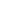What is Poisson's Ratio? -Definition, Formula, Materials & Design

Poisson's ratio is one of the main properties of material that describe relationships between different types of strain in solid material. It is normally for metals, plastics, ceramics and other materials that have practical applications in engineering and industries. This article will help our customers understand how design optimization depends on Poisson's ratio and how an existing design can be further improved to get maximum efficiency and performance from the material.

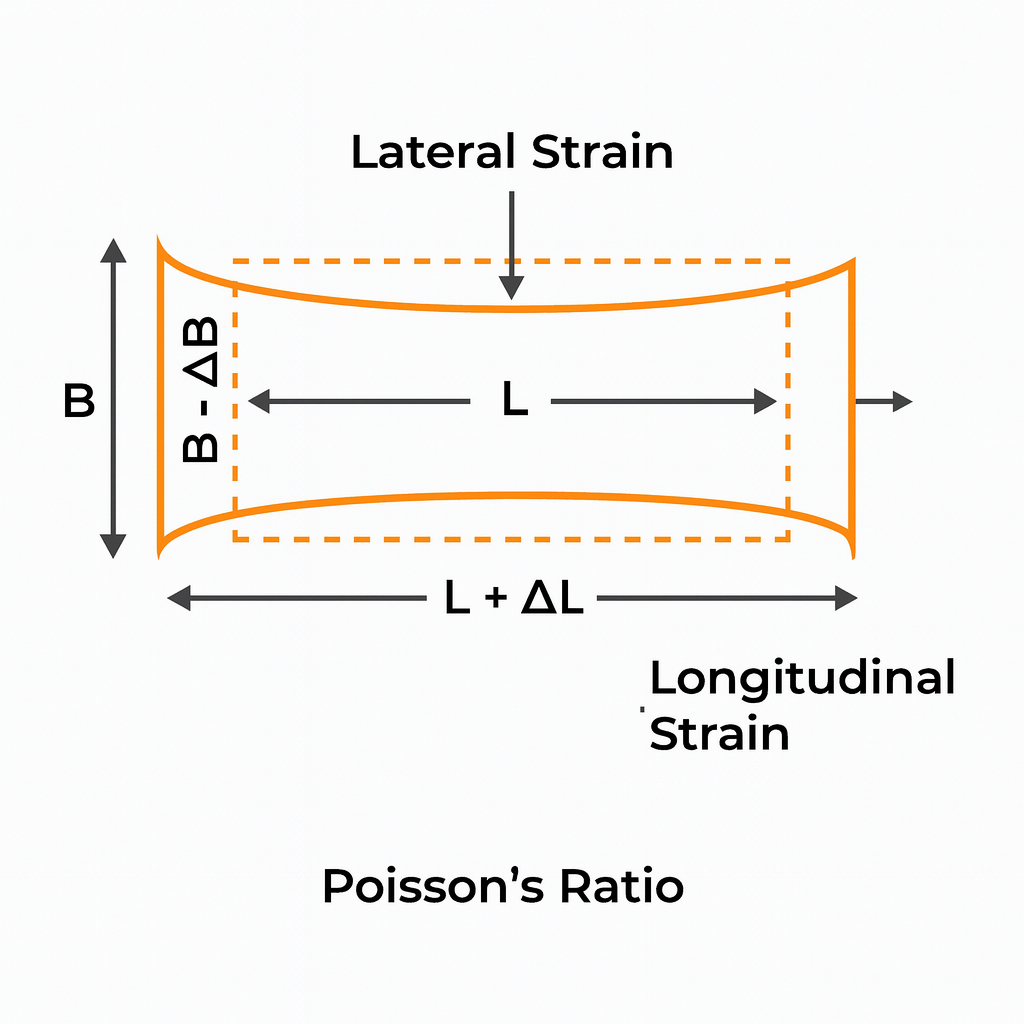
What Is Poisson's Ratio?

Poison's ratio describes the Poisson effect of a material during expansion or contraction in one direction and its deformation in perpendicular directions from corresponding or opposite expansion or contraction.

Why Is Poisson's Ratio Important?

Poison's ratio is important in structural designing, deformation analysis and in material selection. It is a key elastic property in engineering to understand the material's behavior under stress, its deformation in perpendicular direction to prevent failure. It is also used in civil engineering and mechanical engineering to determine stress and analyze the beams, plates and geological formations response to loads.  

Poisson's Ratio Definition in Engineering

It helps to understand the elastic deformation in material when uniaxial stress is applied. Poison's ratio is used for anisotropic material like composites. It typically ranged from 0-0.5 and it helps to understand the curvature in perpendicular direction to the applied load.

Brief History

In 1807, Thomas Young was the first one who drew attention to the mechanism of lateral deformation under longitudinal stress. It was later formalized as mathematical relationship. It is still used today to develop new materials and analyze existing ones.

Who First Defined Poisson's Ratio?

In 1828, Siméon Denis Poisson formularized the relationship between the deformation to define the Poison's ratio which is named after him

Poisson's Ratio in Engineering

In engineering, Poison's ratio is related to Young's modulus (E), Shear Modulus (G) and Bulk Modulus (K) by the equations that connect elastic properties.

Relationship with Other Elastic Constants

The relationship between Poison's ratio and other Elastic constants are as:

Young's Modulus and Shear Modulus

Poison's ratio is related with these moduli for isotropic material. The Poison's ratio formula that connects it with these moduli are:

E=2G (1+v)

Where E is elastic modulus, G is shear modulus and v is Poison's ratio.

Bulk Modulus and Compressibility

Poison's ratio is related to bulk modulus and Young's modulus. Poisson's ratio formula with bulk modules and Young's modules are:

K=E/3 (1-2v)

Bulk modulus is the measurement of material's behaviors when uniform pressure is applied like sinking in liquid. Compressibility is the reversed of bulk modulus (1/K) . That means higher the bulk modules, lower the compressibility.

How to Calculate Poisson's Ratio from Young's Modulus

If the shear stress is known, Poison's ratio from Young's modulus can be calculated. Poisson's ratio formula is:

G=E/ (2(1+v))

By rearranging the formula, Poisson's ratio from young's modulus is:

2G (1+v)=E

1+v=E/ (2G)

v= (E/2G) -1

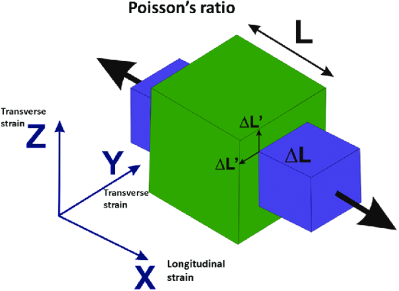
How to Calculate Poisson's Ratio from Stress Strain Curve

To calculate Poisson's ratio, measure the negative ratio of the transverse strain to the axial (or longitudinal) strain from a stress-strain curve:

v=-(transverse strain/axial strain)

How to Calculate Poisson's Ratio from Tensile Test

To measure the Poison's ratio, calculate the longitudinal strain that is along the force direction and the transverse strain that is perpendicular to the force during the tensile test using the formula:

v=-(transverse strain/longitudinal strain)

How to Calculate Poisson's Ratio

Poisson's ratio (v) is the measurement material deformation perpendicular to applied force.

Lateral vs Axial Strain

These strains occur when the material is subjected to load in one direction. Axial strain (ϵ_l) is the deformation that occurs parallel to the direction of the applied force and the lateral strain (ϵ_t) is the deformation that occurs perpendicular to the applied force.

Calculation Formula of Poisson's Ratio

The Poison's ratio formula is written as:

v= - ϵ_t / ϵ_l

where v is Poisson's ratio, ϵ_t is the transverse (lateral) strain, and ϵ_l is the axial (longitudinal) strain. 

Step-by-Step Calculation Guide

To calculate the Poison's ratio for a material, follow these steps:

1. Measure the original dimensions, the length L₀, and the diameter d₀ of the material.
2. Apply load and calculate the new dimensions, new length L_n and new diameter d_n .
3. Measure the axial strain ϵ_l with the formula:

ϵ_l = ΔL / L₀ = (L_n - L₀) / L₀

4. Measuer the lateral strain ϵ_t with the formula:

ϵ_t = Δd / d₀ = (d_n - d₀) / d₀

5. Now measure the Poison's ratio with the formula

v= - ϵ_t/ϵ_l

Typical Values of Material Class

Each type of material has different values of Poison's ratio depending on the behavior of material when stress applied.

What Is the Critical Value of Poisson's Ratio?

The critical value of Poison's ratio is observed in isotropic material, 0.5. This value indicates the material is incompressible now and volume will not change under stress applied.

Which Material Has the Highest Poison's Ratio?

Lateral deformation and incompressibility in any material helps to define the value of poison's ratio in any material. high ratio means material will contract in transverse direction

What Is Poisson's Ratio for Steel?

The Poisson's ratio of Steel is 0.27-0.30. This can be changed slightly based on the composition and processing. This range is standard for many grades like 304, 316 or 416.

What Is Poisson's Ratio of Aluminum?

Poisson's ratio of aluminum is 0.31-0.34 that is higher than steels. For others like Poisson's ratio of aluminum 6061 t6 has 0.33 value. Higher value of aluminum means material becomes thinner when it expands from one direction, and it bulges out when it is compressed.

What Values Are Not Physically Possible

Poison's ratio must be ranged from -1 to 0.5 for isotropic materials. Values greater than 0.5 or less than -1 are not physically possible.

What Does a Poisson's Ratio of 0.5 Mean?

The value close to 0.5 means that material is incompressible now. This value is for softer materials like rubber. This is the maximum value for isotropic material.

How to Measure Poisson's Ratio

Poison's ratio is measured by Tensile test normally. A uniaxial force is applied to the material and the resultant strain in longitudinal and transverse direction measures the Poison's ratio. But Poison's ratio can be measured by many other methods like strain gauges and extensometers, digital image correlation (DIC) and by dynamic/ultrasonic methods. All these have different working principles and methods of measurement

Strain Gauges and Extensometers

It works by applying load to material and placing one strain gauge in the longitudinal direction and other perpendicular to the load. The transverse strain is measured as:

v= - ϵ_trans / ϵ_axial

This measurement should be carried out in the material's elastic region for accurate results.

Digital Image Correlation

Load is applied to the material which has a random speckled pattern on its surface. images of material are taken by a camera during its deformation. DIC software compares the images and makes graph of strain and displacement across the surface. Then, Poisson's ratio is calculated from this data.

Dynamic and Ultrasonic Methods

The speed of ultrasonic waves is used to determine the elastic properties of material including Poisson's ratio. The speeds of wave propagation are measured in longitudinal and transverse directions and related to the elastic moduli. Then, Poisson's ratio can be derived from this data

How Poisson's Ratio Changes Part Behavior in Engineering

Poisson's ratio is the measurement of deformation of material in perpendicular to the applied force. It is important for the scenarios where it dictates how much a material expands or contracts when pressurized. Poison's ratios affect the performance of material under load. It is a key factor in calculating axial stress which affects the stress distribution in the component.

Interference Fits and Seals

Poison's ratio determines the transverse expansion of part when it is compressed axially. Higher poison's ratio means high transverse expansion at the given axial compression. It is important to create tight seals. poison's ratio is related to the deformation ability of material under pressure without getting damaged. The ratio close to 0.5 means material can deform at large volume.

Thin-Wall Stability and Buckling

Normally, materials have poison's ratio between 0.2 and 0.3 which highly affect the lateral deformation of part under compressions. For example, composite laminates have negative ratio which increases the buckling strength of thin-walled structure. The negative value means high stability in structure. Other factors like geometry also affect the aspect ratio and the presence of holes or other features of the thin-walled part.

Pressure Vessels and Pipe Stress

Poison's ratio value affects overall stress-strain behavior and its ability to survive pressure in pressure vessels or pipes. The hoop stress in pressure vessels is twice the longitudinal stress, and this affects Poisson's ratio in both directions. While pipe has both longitudinal and circumferential stress due to pressure and temperature changes. Poisson's ratio calculates the resulting deformation in both directions in pipes.

Main Factors Affecting Poisson's Ratio

There are many factors that affects the poison's ratio in material like temperature, loading rate, moisture content, and microstructure/anisotropy. Their effects are explained below on Poison's ratio

Temperature Effects

Higher temperature decreases Poisson's ratio in many materials. This is due to increased molecular mobility and decreased stiffness. Thermal expansion also indirectly affects the deformation of material under load and thus influencing Poisson's ratio.

Loading Rate Effects

Heavy loading rates increase Poisson's ratio. This is due to the more dynamic nature of deformation in materials with viscoelastic properties.

Moisture Effects

Porous materials like concrete have high moisture content and thus higher Poison's ratio. Water fills the pores and softens the material.

Microstructure and Anisotropy

Grain shape, size and orientation affect the mechanical properties and Poison's ratio of material depending on the loading direction related to the microstructure. In anisotropic materials, Poisson's ratio is different due to the direction of the applied stress related to the crystallographic axes.

When Poisson's Ratio Matters Most

Poisson's ratio is important property in applications where material deformation under stress is a major concern.

Auxetic Materials for Energy Absorption

These are negative Poisson's ratio materials. Auxetic materials become thicker in perpendicular direction when stretched. This feature increases their energy absorption property. They can absorb and dissipate impact energy over a larger area and are used in packaging, and biomedical implants.

Nearly Incompressible Rubbers

Poison's ratio ≈ 0.5 means the volume of material is constant when deformed. This feature mostly found in elastomers and rubbers and are almost incompressible. They are mostly used in seals and gaskets to retain volume under pressure

Composites and Formed Metals

In anisotropic materials like composites or formed metals, Poison's ratio is directional. Its value changes in the direction in which stress is applied. This feature is important in designing layered or reinforced materials to determine the overall behavior of material by the orientation.

Conclusion

Poisson's ratio is a mechanical feature in a material that determines the ratio of transverse strain to the axial strain in a material when it is stretched or compressed. Material becomes thinner when it is stretched lengthwise and it expands laterally when compressed. This means positive axial strain leads to negative transverse strain and negative axial strain leads to positive transverse strain. The Poison's ratio formula has negative sign which shows common materials have positive Poisson's ratio.

Looking for a service provider to customize your design, "Get Your Free Project Quote from TUOFA CNC machining service”.

FAQs

What does a zero Poisson's ratio mean?

Poison's ratio with zero value means the material will not change its volume when stretched or compressed longitudinally.

What does a negative Poisson's ratio mean?

Negative Poisson's ratio materials mean material will expand in transverse direction when it is stretched longitudinally, and contracts laterally when compressed.

What is the unit of Poisson's ratio?

Poison's ratio is a dimensionless quantity. Thus, it has no unit

Is Poisson's ratio the same as depth?

No, Poison's ratio changes with the depth.it describes a material's response to stress, while depth is a measure of physical location.