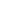Understanding and Calculating Young's Modulus: Step-by-Step Guide

In material science and engineering evaluation of materials mechanics properties is crucial. Young’s modulus is the measure of a material's ability to deform elastically under tensile stress. young’s moduli or tensile elasticity helps material scientists to evaluate the stiffness of a material. In this article, you will get to know the importance of Young's modulus and how to calculate Young's modulus.

Introduction to Young's Modulus

In service life material has to face different loads. So as a material engineer, you have to select a material that can bear all the forces without breakage in service life. Young modulus calculation or tensile elasticity would help scientists evaluate how stiff the material is by calculating the slope of stress /strain. The behavior of material under different forces and loads can be predicted by specific modulus behavior.

History

Hooks law of Roberts Hooke states that the strain is directly proportional to the stress applied within an elastic limit. This Hooks law is the groundwork laid for material tensile elasticity properties. Thomas Young later defined the term young modulus and provided mathematical formulas by calculating the slope for how the material behaves under stress. He introduces tensile elasticity modules of material which later become Young's modulus.

Thomas Young

Units and Symbols

“E” is the Youngs modulus symbol. The unit for Young's modulus or stiffness unit is N/m² (Newtons per square meter) also known as Pascal. For larger values, it is measured in GPa (GIGA Pascal) where GIGA is a prefix that is equal to.

1GPa=

Types of young's modulus

Different types of young modulus are described below. The difference is due to the change in force applied.

Tensile Modulus: This specific modulus is the most common form of Young's modulus. It is also called tensile elasticity. The stiffness is measured when uniaxial tensile stress is applied to the material.

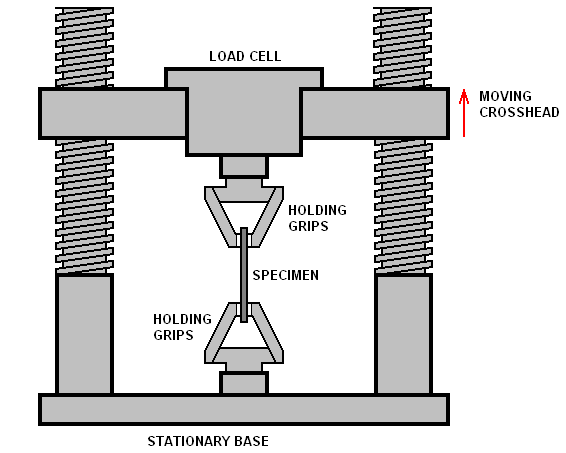
Image of the tensile test setup.

Flexural Modulus: This specific modulus is calculated when the material is bent. The structural components and beam application require this flexural stiffness measure.

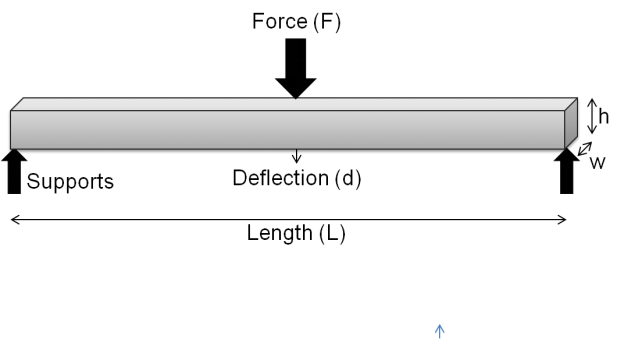
Image for the flexural stiffness test specimen.

Shear Modulus: This specific modulus is calculated before the material undergoes plastic deformation when subjected to shear stress. This modulus is known as the shear modulus. The poisons ratio is related to the shear modulus. The shear modulus is important for applications where the material has to work under shear force.

Image for specimen undergoing shear force.

Bulk Modulus: The stiffness of material measured when undergoing uniform compression force. Through the poisons ratio, the bulk modulus is related to Young's modulus and shear modulus. This specific modulus is important for calculating the slope of compressional stress over compressional strain.

Image showing compression test for bulk modulus calculation on concrete brick.

What does Young's modulus measure?

Young's modulus is a calculation of material elasticity which is stress over strain value in the elastic region of stress-strain tensile curve before plastic deformation. In general, we can say that Young's modulus describes the stiffness of the material.

Young's modulus values

Young's modulus value varies greatly with the material. Some Young's modulus values are given below for different random materials.

• Rubber young’s modulus is approximately equal to 0.01-0.1 GPa.
• The low-density polyethylene Young's modulus is approximately equal to 0.11-0.86 GPa.
• Diatom solid Young's modulus is approximately equal to 3-3.5 GPa.
• Polystyrene foam Young's modulus is approximately equal to 2.5-7 × 10^ (-3) GPa.
• Medium-density fiberboard (MDF) Young's modulus is approximately equal to 4 GPa.
• Wood (along the grain) Young's modulus is approximately equal to 11 GPa.
• Human cortical bone Young's modulus is approximately equal to 14 GPa.
• Carbyne Young's modulus is approximately equal to 1000 GPa.

Benefits and Downsides in Calculating Young's Modulus?

The general advantages and disadvantages of calculating Young's modulus are given below.

Young's Modulus of Various Materials

The stiffness measures of different materials including plastics and metals are given below.

The Science Behind Young's Modulus

Calculating slop of stress/strain when tensile test across specific cross-section area is performed for Young's modulus. These calculations involve values of stress and strain.

Elasticity: Elasticity is the ability of a material to retain its original shape and size after tensile force is removed. This calculation for young modulus is done before elastic deformation occurs.

Stress and Strain

Stress is the uniform force applied through a specific cross-section area of a specimen to produce strain in it is called stress. Strain is the elongation of the material through a cross-section area. Elongation causes a change in the shape and size of the original shape of the material.

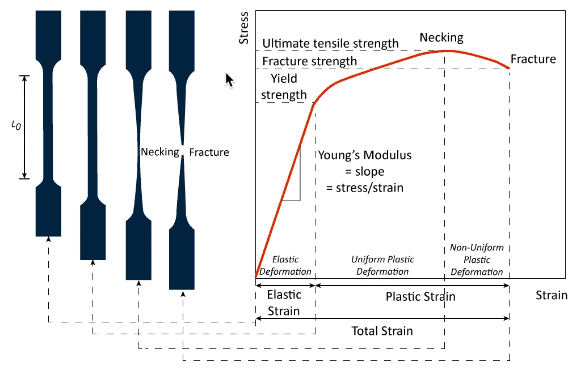
The image above shows complete changes in the specimen undergone tensile test and stress vs strain curve for the specimen.

The Formula for Young's Modulus

Young modulus can be calculated from the formula given below

Basic equation

Elasticity=

Or

Elasticity= ×

Variable Explained

Stress is equal to the tensile force applied during the test divided by the cross-section area of the specimen on which force is applied. Strain is the ratio of the original size of the specimen taken for the test to the length change during the test when stress is applied.

How to Calculate Young's Modulus: Step-by-Step Guide

The calculation of the young modulus can be done using formulas. The method of calculating Young's modulus is given below.

Step 1: Measuring Stress - Methods to measure the force applied.

UTM would apply tensile force on the sample. The applied force is measured using force transducers or load cells. To measure force load cells are integrated into different testing samples. load cells convert mechanical force to electrical signals.

Step 2: Measuring Strain - Techniques to measure deformation.

Strain gauges measure the change in length in minutes of a specimen. As the material compresses or stretches it changes electrical resistance. The change in length of the material between two points can be measured from extensometers.

Step 3: Applying the Formula - How to use the measured values in the formula.

For stress calculation use the formula given below in which "F" is the force and "A" is the respected area.

σ=A/F

For the calculation of strain ε use the formula below where ΔL is the change in length where L0 is the original length.

ε= ΔL/ L0

The Young's modulus would be calculated from the formal given below:

Elasticity=

Example Calculations

Example 1: The cross-sectional area of a rod is 1 cm² when the tensile force of 10 kN is applied to it. 50 cm is the original length while elongation of 0.05 cm is seen when load is applied.

Given:

• F = 10 kN = 10,000 N
• A = 1 cm² = 0.0001 m²
• L₀ = 50 cm = 0.5 m
• ΔL = 0.05 cm = 0.0005 m

Formulas:

σ=A/F

10,000 N/0.0001 m²=100 MPa is the stress.

ε= ΔL/ L0

0.0005 m/0.5 m =0.001 is the strain.

Elasticity=

100 MPa/0.001 =100 GPa is the young’s modulus of the rod.

Example 2: A concrete beam with a cross-sectional area of 0.05 m² is subjected to a compressive load of 500 kN. The original length of the beam is 2 m, and the compression under the load is 0.2 mm.

Given:

• F = 500 kN = 500,000 N
• A = 0.05 m²
• L₀ = 2 m
• ΔL = 0.2 mm = 0.0002 m

Why Young's Modulus Matters

Young's modulus defines the stiffness of the material which is crucial for applications where material has to undergo excessive loadings and impacts.

Material Selection

For applications where stiffness and elasticity are the key considerations, Young's modulus is particularly important. For high-stiffness applications, steel can be chosen because it has a high Young's modulus. Application where flexibility is the key consideration rubber can be chosen because it has a low Young's modulus.

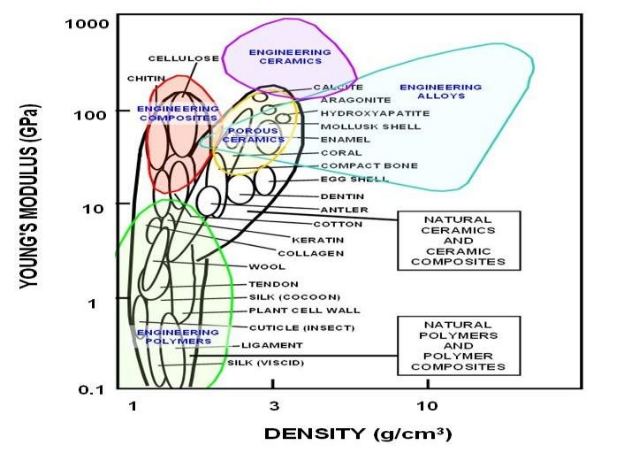
Varied materials concerning Young's modulus and density are given for material selection for specific applications.

Structural Analysis

The structure behavior under load can be predicted by Young's modulus in structural engineering. Some use the full advantages of Young's modulus in structural analysis.

• Buildings, bridges, and other such structure analysis and design.
• Under load columns and beams deflection analysis.
• Serviceability and safety assessment of structures.
• Structure design optimization.

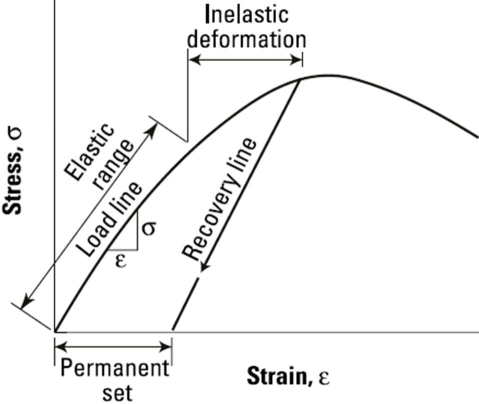
Young modulus of concrete.

Mechanical Properties

Mechanical properties like ductility, hardness, and tensile strength are co-related with Young's modulus.

Applications of Young's Modulus

The calculation of Young's modulus helps material engineers to select the best material for the desired application. In every industry where the material has to go through different loads and fatigue cycles during its service life, Young's modulus value matters a lot.

Automotive: Automotive components that have to undergo various loads like stresses, impacts, and vibration can be designed with the help of a young modulus. Applications require elastic properties like body panels, suspension systems, and frames .

Construction: In construction Young's modulus helps in the analysis and design of bridges, buildings, and other structural components. Elastic properties allow durability and optimal performance of the structure.

Concrete bridge.

Aerospace:

Elastic properties, poison ratio, shear modulus, Young's modulus, and other specific modules are required for studying each component of aerospace. As high-tech applications like aerospace detail analysis of each material's mechanical properties are required for optimal design and performance of components. Young's modulus is helpful in the material selection of aerospace components because the material has to go through thermal stresses, shear loads, and different flight loads.

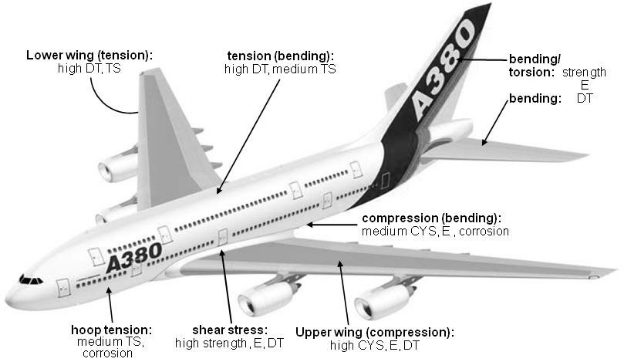
Different load conditions on different parts of aerospace are shown.

Factors Affecting Young's Modulus

There are no factors that affect the young’s modulus value. Diverse types of material would have different microstructures and have different young modulus. Temperature, pressure, radiation, and humidity also cause changes in the value of Young's modulus of material.

Material Composition

Diverse materials have different Young's modulus some of Young's modulus for different types of materials is given below.

Types of Materials:

Microstructure: How the microstructure of a material influences its Young's Modulus.

Environmental Factors

Temperature: Increased temperature increases molecules' vibration so decreases Young's modulus value. While the decrease in temperature makes the material stiffer so increases Young's modulus value.

Pressure: High pressure increases interatomic spaces and increases the strength of bonds so increases Young's modulus. Low pressure decreases Young's modulus because less constraining in atomic bonding is seen.

Measuring Young's Modulus in the Tuofa Machining Lab

Tuofa machining lab has the best precise equipment which is used for the measuring of Young's modulus. The equipment is precise and up to date.

Get more information about Tuofa Lab from the website.

https://www.tuofa-cncmachining.com/

Equipment and Tools

For the tensile test and Young's modulus calculation following equipment is used.

Universal Testing Machine: This is used to perform tensile tests. With the help of UTM, the uniform tensile load is applied to the sample

UTM image.

Force transducers or load cell: Measure applied force by converting mechanical signals to electrical signals.

Load cell or force transducer.

Strain Gauges: Measure the change in length of the specimen after the force is applied.

Strain Gauge image.

Testing Methods

Testing methods depend upon the force applied. The following are the testing methods:

Tensile Test: uniaxial tensile force is applied along the cross-section area of a specimen. The force causes a change in the original shape of the specimen. The change in length is measured by a strain gauge. The strain-strain graph is plotted from force/area values obtained from the test. Calculating the slope of the stress-strain curve helps you to determine different mechanical properties including Young's modulus .

Flexural Test: This is performed by applying bending force on the specimen. The specific modulus determined from this test is called flexural modulus.

Compression Test: uniaxial compression force is applied along the cross-section area of a specimen. The force causes a change in the original shape of the specimen. The decrease in length is measured by a strain gauge. The strain-strain graph is plotted from force/area values obtained from the test. Calculating the slop of the stress-strain curve helps you to determine different mechanical properties including Young's modulus.

Conclusion

It is concluded that mechanical properties play a key role in material selection. Young's modulus is one of the important mechanical properties which determine the stiffness of the material. The applications like construction, automotive, and aerospace where the material has to face different vibrations, stresses, and impacts Young's modulus value is particularly important. For high Young modulus requirement material like steel is used while for low Young's modulus but flexible material, rubber is the best choice.

FAQ

Is a higher Young's modulus stronger?

No! young’s modulus and strength are related but it does not mean higher Young's modulus material is stronger. Young modulus is a mixture of both elasticity and strength of material which is why defined as the stiffness of material.

Is Young's modulus the same as elasticity?

No! young’s modulus and elasticity are related but they are not the same. Young modulus is a mixture of both elasticity and strength of the material which is why defined as the stiffness of the material.

Young's modulus vs bulk modulus

Young's modulus is calculated when material is subjected to tensile load while bulk modulus is calculated when material is subjected to compression load.