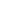What is Shear Modulus: 7 Models Predict for Metal

When mechanical properties of any material are analyzed, the important parameters like stress and strain relationship are considered. These parameters provide valuable insight in the material's behavior towards different forms of stresses. Among them, shear modulus is an important feature in material. This occurs by applying stress in a specific direction. This piece of writing will provide detailed information about the shear modulus along with how it affects the material's processing and applications. This will also help in the selection of material for any particular application under the action of different loading conditions .

Fundamental Concepts

Shear or Modulus of rigidity are common terms of same phenomena. This measures the rigidity in an object when a shear force is applied. The ability of an object to resist the deformation is determined by shear modulus. Different loading conditions parallel to the surface of the object are applied in this event.

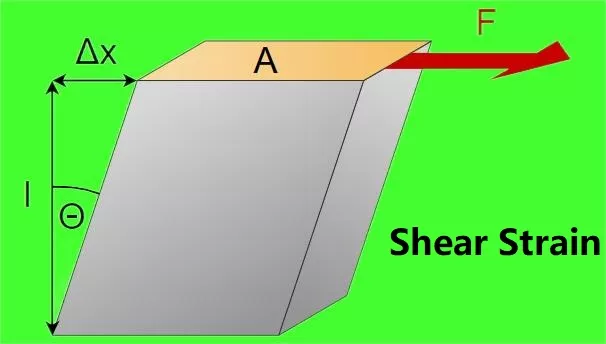
Shear forces introduce shear strains in the object. Shear modulus is determined by the dividing stress over strain. This parameter is important for structural analysis in engineering. Because it explains the response of material in the application of forces to determine the mechanical properties

What is Shear Modulus

Shear modulus determines the stiffness in material when shear forces are applied. It helps to determine the endurance to twisting deformation. This occurs in the area under the elastic region in stress-strain curve. High the shear modulus, higher the shear forces for endurance and rigidity. A low shear modulus shows less rigidity. This means the material is vulnerable to twisting deformation.

Shear modulus is written as:

G = τ / γ

Where, G is the shear modulus. τ is shear stress. γ is the shear strain.

The units of shear modulus are pressure. It is denoted as Pascal (Pa), Pounds/square inch (psi).

Shear Modulus and Related Moduli

The elastic modulus of an object is like Young's modulus or bulk modulus and shear modulus. All are related to Hook's law. This law defines the strain that occurs in a material by applying the stress. And it is directly proportional to stress. The relationship between all these moduli with shear modulus is explained this term below:

2G(1+υ) = E = 3K(1−2υ)

Where, G is the Shear Modulus. E is the Young's Modulus. K is the Bulk Modulus. And υ is Poisson's Ratio.

From Hooke's Law to Shear Modulus

Hook's law is used to obtain the shear modulus. Consider the shear stress and corresponding strain developed in the material. stress is the applied load which direction is parallel to the surface. strain occurs in the material is at the angle of deformation of material. To know the stiffness, stress would be divided by the strain same as in the Hook's law.

7 Models are Used to Predict the Shear Modulus of Metals

There are few models to predict the shear modulus in a material. the models used in plastic flow computations are explained below:

Mechanical Threshold Stress (MTS) Model

The flow stress under different temperatures and strain rates are determined with the help of this model. This model is applied to describe the response of a material when extreme conditions of temperature and forces are applied.

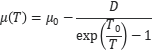
Where,  represents shear modulus at temperature T while other values are constant.

Steinberg-Cochran-Guinan (SCG) Model

This is an empirical model. It describes the mechanical response of materials when high strain and temperature are used. The analysis of metals with high temperature and flow stress are conducted by using the formula:

Where,  represents shear modulus at temperature T. and P is pressure.

Nadal and Le Poac (NP) Model

This is modification of SCG model. It predicts the metal behavior precisely when different strain rates are applied and explains temperature dependence feature.

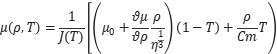
Johnson-Cook Model

It was initially used for flow stress prediction. But later it was modified to predict the shear modulus of metals under various strain rates and has temperature dependence feature.

Where,  represents plastic strain rate.  is the reference strain rate.

Zerilli-Armstrong Model

This model describes the metal behavior under different strains and has temperature dependence feature. strain. And provides information about the shear modulus of metal.

Arrhenius-Type Models

This model describes the metal with temperature dependence application. This helps in analyzing the effect of shear modulus of metal when different temperatures are applied.

Practical Applications in Manufacturing

Shear modulus has a great effect on the mechanical characteristic of an object. And it influences the material selection in engineering applications. Different properties are considered such as resilience, young’s modulus, strain rate, material stiffness or deformation depending on the applications. Metals with high material stiffness have high deformation resistance. These are most suitable for structural engineering applications. Metals having greater shear modulus values are also suitable for automotive and construction fields.  While metals with low material stiffness have high capacity to absorb energy such as rubber.  They have high flexibility and elastic modulus or young’s modulus values. They have most applications in coupling metals between rotating shafts. Metals that have high rigidity and are more resistant to shear deformation are mostly used in beams, bridges and structural components in construction.

Material Selection in CNC Machining

Any metal or plastic material can be produced by using CNC machining. Metals mostly have high shear deformation resistance than plastics. Depending on the applications, any part can be produced in TOUFA CNC machining services by CNC machining and turning. Metals like a variety of steels, aluminum, copper and its alloys are being manufactured in TUOFA. Selection of the right material for high or low shear deformation resistance can be challenging. because it is important to understand the pros and cons and best use of the material. but TUOFA has years of experience and qualified and skilled labor and engineers that can help you in selecting the right material for your project. Some important factors to consider during the selection of right materials are as:

• Applications: it is necessary to know the use of material and its purpose to produce.
• Operating Environment: it is an important factor to know the surrounding environments and other factors like strain rate, loads and temperature is very important to know before material selection.
• Tolerance and Dimensional Stability: you must know the allowance of tolerance during the material application.
• If a material has low machinability, it would be difficult to manufacture the material with high performance and efficiency.
• Material Costs. It is always the important factor in any stage of material selection and application.
• If a material is not readily available, the application of material would be limited.

Calculating Shear Modulus: A Detailed Guide

To explain the shear modulus mathematically, it is expressed in terms of ratio of shear stress or to shear strain. Shear stress becomes the shear force applying on the per unit area of an object. Shear strain becomes the ratio of change in length to initial length. Shear strain is the corresponding deformation occurring at the tangent (tan)angle theta θ. This represents the change in length at the right angle 90ᵒ. To explain the shear strain mathematically, tan θ is used which is equal to x/y.

This formula represents the special forms of Hook’s law. The denominator is a dimensionless quantity. And the dimension of shear force is the force acting per unit area.

Shear Modulus in Different Materials

Shear modulus represents the rigidity of material. It shows the resistance to deformation occurs by shear forces. The highest value of shear modulus is of the diamond which is 520GPa. All the metals have shear modulus in the range of 10-80GPa. For polymers and rubbers, shear modulus is below 1GPa.

The shear modulus in different materials is shown in the table below:

Comparing Shear Modulus Across Materials

Different objects have different shear modulus. To understand the comparison between the shear modulus in the objects, an example is presented here. This will identify the comparison and will help to define the rigidity of material.

The shear modulus of wood is 6.2 x108Pa. steel has 7.2x1010 pa shear modulus. This means steel has way more rigidity than wood. It is around 127 times higher than wood.

Advanced Concepts in Shear Modulus

To know the shear modulus, there are many techniques available. Common advance method is static torsion method. It is conducted by a torsion pendulum. Or sometimes a rod is twisted directly over the object. ASTM-D-2236 standard is used in which a hollow cylinder is used. A pendulum is connected to the cylinder, and it is subjected to torsional rotation. The rotation is clockwise and anticlockwise. The shear modulus is calculated by the measurement of period of torsional pendulum.

Another advanced technique is by using material rod in the same static torsion method. The rod is twisted at an angular distance. The resultant stress is determined, and a graph is plotted between stress and strain. This graph provides the data of shear modulus. The standards used are ASTM-E-143 and ASTM-A-938. The first one is for structural materials and later one is metallic wire.

The material which has recorded highest shear modulus is diamond. This is because of covalent bonding between the carbon lattices. The atomic arrangement of carbon is very accurate in diamond. It has cubic Crystal structure and has high compact lattice. This result in high hardness in material. the shear modulus is ranged from 400-500GPa. But diamond is very vulnerable to breakage despite having high hardness. This breakage occurs along the specific plane because of its cleavage feature.

It is interesting to know that some material has zero shear modulus. Any fluid has zero shear modulus which means any load applying to liquid will create deformation without nay resistance.

Conclusion and Further Learning

Modulus of rigidity or shear modulus is a constant value of elastic properties in solid. This occurs by applying stress by traverse internal shear forces. The twisting and torsion in a material around its axis is its rigidity. A very small volume of material is disturbed in these materials. This disturbance is along both faces of that object which is sliding parallel to each other. The distance of this slide is small and the shape of the object changes to diamond from a cube.

Shear modulus describes the material stiffness to survive the flexible deformation. This response of material explains the value of deformity in an object. The object can return to its initial length after removing stress. But if excessive stress is applied, the material can be permanently deformed or rotated or maybe failure or materials can occur.

The modulus of rigidity measuring material stiffness with the help of Hook’s law same as the Young’s modulus.

Young’s modulus is a measure of ratio stress to strain. it is a uniaxial stress like pulling the wire from both ends. Shear modulus of elasticity is the response of shear forces. And the force acts in angular direction and for isotropic objects.

Modulus of rigidity is related to the solid state when the shear force acts on of its surface and the other end of object has opposite forces. The materials with anisotropic features like wood and all the single crystal material will show different response to shear force when the force acts in different direction. All the materials have different concepts of shear modulus of elasticity. But the concerned part is their mechanical properties. Selection of the right material for high or low shear deformation resistance can be challenging. because it is important to understand the pros and cons and best use of the material. But TUOFA CNC machining service has years of experience and qualified and skilled labor and engineers that can help you in selecting the right material for your project. Depending on the applications, any material can be produced in TOUFA CNC machining services by CNC machining and turning.